As Cevianas notáveis e especiais de um triângulo: Altura, Mediana e Bissetriz.

by Roberto M.

O que são cevianas?

Em vários outros artigos já tivemos oportunidade de falar sobre triângulo.

Já vimos como construir um triângulo qualquer, como classificar um triângulo quanto aos seus lados ou como classificar um triângulo quanto aos seus ângulos internos. Vimos também qual é a condição de existência de um triângulo, bem como quais são seus principais elementos.

Sabemos que os elementos básicos de um triângulo são os vértices, os lados e os ângulos. Entretanto, eles não são os únicos. Hoje vamos falar de uma outra família de elementos que podemos identificar em um triângulo qualquer: as cevianas.

CEVIANAS

Definimos ceviana como sendo qualquer segmento de reta que une um dos vértices do triângulo à reta suporte do seu respectivo lado oposto.

Qualquer segmento que tenha essas características é uma ceviana.

Na figura acima, vemos exemplos de cevianas que partem do vértice A do triângulo ABC. Da mesma forma, existirão cevianas partindo dos vértices B e C.

O nome ceviana é uma homenagem ao matemático italiano Giovanni Ceva (1648-1734), que demonstrou teoremas importantes sobre as mesmas.

Entretanto, existem três dessas cevianas que possuem características especiais e, por isso, recebem nomes especiais.

São elas: altura, mediana e bissetriz.

Vamos explicar as características de cada uma delas:

ALTURA

A altura é uma ceviana especial que sai de um determinado vértice e tem a característica de ser perpendicular à reta suporte do lado oposto.

Na figura acima vemos a altura relativa ao vértice A e lado BC.

Analogamente, teremos as alturas relativas ao lado AC (vértice B) e ao lado AB (vértice C).

MEDIANA

A mediana é uma ceviana especial que sai de um determinado vértice e tem a característica de ir até o ponto médio do lado oposto.

Lembre-se que ponto médio é o ponto que divide o segmento em duas partes iguais, ou seja, é o ponto que fica exatamente no meio do segmento.

Na figura acima vemos a mediana relativa ao vértice A e lado BC.

Analogamente, teremos as medianas relativas ao lado AC (vértice B) e ao lado AB (vértice C).

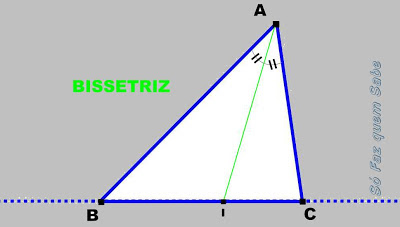
BISSETRIZ

A bissetriz é uma ceviana especial que divide o ângulo interno, relativo a um determinado vértice, ao meio, ou seja, em duas partes iguais.

Na figura acima vemos a bissetriz do ângulo A.

Analogamente, teremos as bissetrizes relativas ao ângulo B e ao ângulo C.

CONCLUSÃO

- A partir de cada vértice partem infinitas cevianas.

- Por terem características especiais, três dessas cevianas recebem nomes especiais.

- Altura: sai de um vértice e é perpendicular ao respectivo lado oposto.

- Mediana: sai de um vértice e vai até o ponto médio do respectivo lado oposto.

- Bissetriz: sai de um vértice e divide o ângulo interno, relativo a esse vértice, ao meio.

- Como o triângulo tem três vértices e, de cada vértice saem cevianas, deduzimos que todo triângulo tem três alturas, três medianas e três bissetrizes.

Nos próximos artigos veremos como traçar geometricamente as alturas, as medianas e as bissetrizes de um triângulo. Acompanhem.

Artigos Recomendados:

• MEDIANAS quando cruzam, formam o BARICENTRO do triângulo, um ponto notável.
• Das ALTURAS do triângulo obtemos o ORTOCENTRO, um ponto notável.
• BISSETRIZES de um triângulo geram o INCENTRO. Um ponto notável, centro da circunferência inscrita.
• CIRCUNCENTRO da circunferência circunscrita. Ponto notável do triângulo gerado pelas MEDIATRIZES.
• Bissetriz de um ângulo. Aprenda a traçar.
• Conceito de ângulo e de sua medida.
• Mediatriz de um segmento de reta. Aprendendo a traçar e a obter o ponto médio.
• Polígono. Classificação e Nomenclatura.
• Como construir um triângulo regular a partir da medida do lado.