Medianas de um triângulo. Como traçar geometricamente.

by Roberto M.

Já estudamos, em outros artigos, os elementos básicos de um triângulo (vértices, lados, e ângulos). Vimos, também, que existe um outro tipo de elemento chamado ceviana e que, existem algumas cevianas que são especiais e notáveis (altura, mediana e bissetriz).

Aprendemos, em um artigo anterior, a traçar a altura de um triângulo. 

Hoje iremos falar sobre a construção geométrica de uma outra ceviana notável, a mediana.

Como visto, quando definimos os conceitos das cevianas especiais, a Mediana é o segmento de reta que liga um determinado vértice de um triângulo ao ponto médio do lado oposto a esse vértice.

Seguindo essa definição, vamos traçar geometricamente a mediana de um triângulo.

Lembrando sempre que, como o triângulo tem três vértices, ele sempre terá três medianas, uma para cada vértice.

Vamos traçar para um dos vértices. Para os outros, a construção será semelhante.

MÉTODO CONSTRUTIVO DA MEDIANA DE UM TRIÂNGULO

Pela definição de mediana, percebemos que, em primeiro lugar, temos que achar o ponto médio de um dos lados e depois uni-lo ao vértice oposto.

Já aprendemos a obter o ponto médio de um segmento de reta quando aprendemos a traçar uma mediatriz, mas, vamos ao passo-a-passo da construção da mediana.

1 – Tracemos um triângulo ABC qualquer

2 - Vamos construir a mediana relativa ao vértice A. Então vamos achar o ponto médio do lado BC.

Vamos pegar o compasso e, colocando a ponta seca no ponto B, com uma abertura maior que a metade do lado BC, traçar um arco que corte BC.

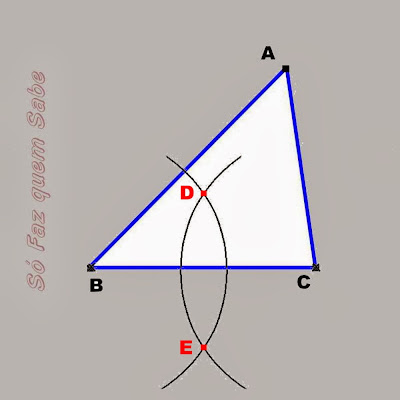
3 – Agora, com a ponta seca no ponto C, mantendo a mesma abertura, traçamos outro arco que intersecte o arco anterior em dois pontos D e E

4 – Ao ligarmos os pontos D e E, a reta obtida (que é a mediatriz de BC) intersectará o lado BC no ponto M, que será o ponto médio que desejávamos.

5 – Ligando-se, agora, o vértice A ao ponto médio M, obteremos o segmento de reta AM, que será a mediana do triângulo relativa ao vértice A que queríamos.

6 – Para traçar as outras duas medianas do triângulo, relativas aos vértices B e C, procede-se de maneira semelhante.

Artigos Recomendados:

• Noções Fundamentais da Geometria. Ideias de ponto, reta e plano.
• Semi-Reta e Segmento de reta. Avançando nos conceitos.
• Classificação de um triângulo quanto aos lados: equilátero, isósceles e escaleno.
• Classificação dos triângulos quanto aos ângulos. Acutângulo, Retângulo, Obtusângulo.
• Conceito de ângulo e de sua medida.