Máximo divisor comum. Aprendendo a calcular MDC.

by Roberto M.
O que é mdc? Como calcular o máximo divisor comum? O que são números primos entre si?
Já sabemos o que é divisibilidade e o que é divisor de um número natural. Leia o artigo para lembrar.
Sabemos também que todo número natural é divisível, pelo menos, por 1 e por ele mesmo. 
Quando o número é divisível apenas por 1 e por ele mesmo ele é chamado número primo. Quando ele tem mais divisores, chama-se número composto. Portanto, podemos dizer que todo número natural possui um conjunto de divisores.

MDC DE DOIS NÚMEROS NATURAIS 

Se pegarmos os conjuntos de divisores de dois números naturais quaisquer, podemos compará-los e verificar quais são os divisores comuns aos dois números, ou seja, aqueles divisores que estão ao mesmo tempo nos dois conjuntos. 

Por exemplo, vamos considerar os números 12 e 18 e os seus respectivos conjuntos de divisores: 

D(12) = {1, 2, 3, 4, 6, 12}

D(18) = {1, 2, 3, 6, 9, 18}

Se fizermos a intersecção dos dois conjuntos, ou seja, verificarmos os elementos comuns aos dois conjuntos, podemos dizer que esses elementos serão divisores, ao mesmo tempo, de 12 e 18. Eles serão os divisores comuns de 12 e 18.

DC(12, 18) = {1, 2, 3, 6} 

Analisando esse conjunto dos divisores comuns de 12 e 18, podemos verificar qual é o maior deles. Descobrimos que o número 6 é o maior divisor comum de 12 e 18. 

Por isso dizemos que 6 é o máximo divisor comum de 12 e 18 e indicamos assim:

mdc(12, 18) = 6 (leia-se: mdc de 12 e 18 é 6). 

Generalizando teremos:

O máximo divisor comum de dois números naturais não nulos A e B é o maior número que é divisor ao mesmo tempo de A e de B. 

NÚMEROS PRIMOS ENTRE SI 

Sempre que o máximo divisor comum de dois números naturais for o número 1, eles serão chamados primos entre si. 

Por exemplo, vamos considerar os conjuntos de divisores dos números 15 e 16:

D(15) = {1, 3, 5, 15} 

D(16) = {1, 2, 4, 8, 16} 

Se compararmos esses dois conjuntos, veremos que o único elemento comum é o 1. Portanto, por ser o único, ele é o maior. Logo, o

mdc(15, 16) = 1 

Assim, os números 15 e 16 são chamados primos entre si.

CÁLCULO DE MDC - Regra das Divisões Sucessivas 

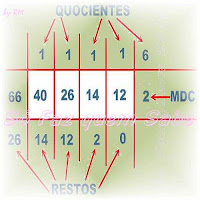
Vamos mostrar a regra prática fazendo um exemplo. Iremos determinar o mdc dos números 40 e 66. Sigamos os passos: 

1) Dividimos o número maior pelo menor

66 : 40 = 1 com Resto = 26 

2) Não dando resto zero, dividimos o divisor pelo resto da divisão

40 : 26 = 1 com Resto = 14 

3) Prosseguimos com as divisões do divisor pelo resto obtido até obter resto zero

26 : 14 = 1 com Resto = 12 

14 : 12 = 1 com Resto =   2 

12 : 2 = 6 com resto = zero 

4) O mdc é o divisor da última divisão efetuada

mdc(40, 66) = 2 

DISPOSITIVO PRÁTICO 

MDC DE MAIS DE DOIS NÚMEROS 

Quando for necessário calcular o mdc de mais de dois números, procedemos da seguinte maneira: 

1) Colocamos os números em ordem decrescente; 

2) Calculamos o mdc dos dois primeiros números; 

3) Depois, calculamos o mdc do resultado encontrado e o terceiro número; 

4) Assim por diante, até o último número da lista; 

5) O mdc é o divisor da última divisão efetuada. 

Exemplo: Calcular mdc(40, 24, 60) 

1) Colocando na ordem decrescente teremos mdc(60, 40, 24)

2) Calculamos o mdc dos dois primeiros números: mdc(60, 40)

mdc(60, 40) = 20

3) Calculamos o mdc do resultado e do terceiro número: mdc(20, 24)

 mdc(24, 20) = 4 

 Logo, mdc(60, 40, 24) = 4 

MDC PELO MÉTODO DA FATORAÇÃO 

Existe outra maneira de calcular o mdc de dois ou mais números. 

Essa maneira consiste em utilizar a decomposição desses números em fatores primos. Quem quiser relembrar como fazer fatoração, veja o artigo “Fatoração de um número natural. “.

Vamos mostrar o modo de calcular o mdc por fatoração através de um exemplo. Iremos determinar o mdc dos números 240 e 252 seguindo os passos:

1) Decompor, separadamente, os números em fatores primos:

240 = 2 x 2 x 2 x 2 x 3 x 5 = 2⁴ x 3 x 5 

252 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7 

2) Verificar os fatores primos comuns a todos os números. 

No nosso exemplo, podemos verificar que o número 2 é um fator comum a todos; novamente o número 2 é um fator comum a todos e o número 3 é um fator comum a todos.

3) O mdc dos números dados é o produto desses fatores primos comuns

mdc(240,252) = 2 x 2 x 3 = 2² x 3  = 12

4) Se observarmos as fatorações dos números escritas na forma de potência, podemos generalizar e dizer que:

O mdc, pelo método da fatoração, é exatamente, o produto dos fatores primos comuns, tomando cada um com o menor expoente que apresenta na fatoração.

Artigos Recomendados:

• Fatoração de um número natural.
• Conjunto dos Números Naturais. O conjunto N.
• Entendendo o que são Sistemas de Numeração.
• Como fazer arredondamento da numeração decimal.