by Roberto M.
Já estudamos, anteriormente, os principais conceitos da “Teoria dos Conjuntos”, tais como:
subconjuntos, elementos, relações de pertinência e relações de inclusão.
No artigo “Fazendo Operações com Conjuntos” vimos as
principais operações que se faz com conjuntos.
Quem quiser relembrar pode ler os artigos citados clicando nos links.
Hoje, com base nos conceitos de par ordenado e plano cartesiano, vamos estudar outra
operação entre dois conjuntos: o produto cartesiano.
Produto Cartesiano de um conjunto A por um conjunto B é o conjunto formado
por todos os pares ordenados, possíveis, obtidos com os elementos de A e de B.
Esses pares são chamados de ordenados à medida que são formados por um
elemento de A e um elemento de B, nessa ordem.
Em outras palavras:
O produto cartesiano de dois conjuntos A e B são todos os pares ordenados (x,
y), onde x pertence ao conjunto A e y pertence ao conjunto B.
Ou seja:
O produto cartesiano é uma relação binária entre os conjuntos A e B de
tal modo que o conjunto A é o conjunto de partida (obtendo x) e o
conjunto B é o conjunto de chegada (obtendo y) obtendo-se, assim,
todas as possibilidades de relações entre A e B.
A representação do produto cartesiano é A x B e, cada elemento
desse produto, é um par ordenado (x, y) obtido como descrito acima.
Note que:
Por serem pares ordenados, os elementos de A x B são diferentes
dos de B x A.
Ao fazermos o produto B x A, o conjunto de partida será B
(obtendo x) e o conjunto de chegada será A (obtendo y).
Para que possamos entender melhor tudo isso, vamos mostrar como se faz e como
se representa a operação “Produto Cartesiano” de dois conjuntos, através
de um exemplo:
EXEMPLO DE PRODUTO CARTESIANO
Dados os conjuntos:
A = {1, 2, 3} e B = {3, 4, 5};
1 - Podemos representar A x B ou B x A através de um diagrama de flechas
mostrando todas as relações possíveis entre os elementos de A com os elementos
de B. Partindo de A e chegando em B ou vice-versa.
Diagrama do Produto Cartesiano A x B
Diagrama do Produto Cartesiano B x A
2 - Podemos representar A x B ou B x A através de chaves, onde podemos ver, mais claramente, os pares ordenados formados devido à relação binária entre A e B.
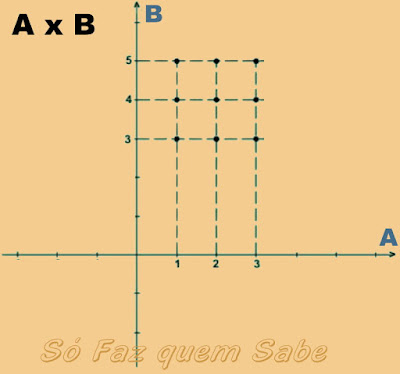
A x B = {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 3), (3,
4), (3, 5)}
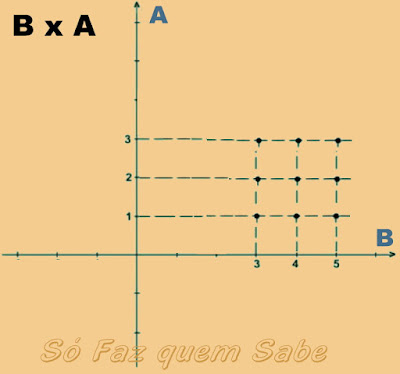
B x A = {(3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3), (5, 1), (5,
2), (5, 3)}
3 - Ou ainda, no próprio Plano Cartesiano, indicando os pontos
representativos de cada par ordenado.
Plano Cartesiano com o Produto A x B
Plano Cartesiano com o Produto B x A
Concluindo, podemos verificar que, no nosso exemplo, o conjunto A tem
3 elementos, o conjunto B tem 3 elementos e o produto
cartesiano entre A e B resultou um conjunto de 9 elementos.
Número de elementos de A => n(A) = 3
Número de elementos de B => n(B) = 3
Número de elementos de A x B => n(A x B) = 9
Matematicamente falando e, sabendo que cardinalidade é o número de elementos de um conjunto, dizemos que: a cardinalidade do conjunto A é 3; a cardinalidade do conjunto B é 3;
resultando um conjunto A x B de cardinalidade 9.
Isso pode ser generalizado para qualquer produto cartesiano.
O número de elementos do produto cartesiano de dois conjuntos A e B (ou seja,
todos os pares ordenados formados pelas relações binárias entre A e B), será
sempre o resultado da multiplicação entre o número de elementos de A e o número
de elementos de B.
n(A x B) = n(A) x n(B)
Se tiver interesse, leia o artigo que fala sobre o “Plano cartesiano e seus pares ordenados”.
esta muito bom
ResponderExcluir