by Roberto M.
Como fazer para dividir uma circunferência qualquer em cinco partes iguais?
Como é que se inscreve um pentágono numa circunferência?
Como se faz par construir um pentágono regular?
Como é que se inscreve um pentágono numa circunferência?
Como se faz par construir um pentágono regular?
Quando dividimos uma circunferência em cinco partes iguais, os cinco pontos que achamos são também os vértices do pentágono regular inscrito na circunferência.
Vamos, então, pegar papel, lápis, régua, compasso e aprender a fazer essa construção geométrica. É só seguir os passos abaixo:
Passo 1
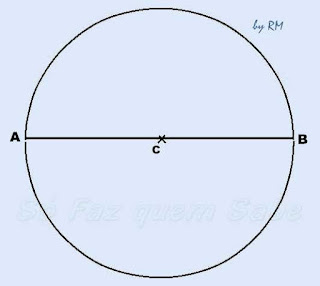
De início, vamos traçar uma circunferência. Marcamos um ponto C no papel e, com um compasso, traçamos uma circunferência com centro nesse ponto C e com um raio qualquer.
Passo 2
Com uma régua, traçamos um diâmetro da circunferência e marcamos os pontos A e B.
Passo3
Agora, vamos traçar um diâmetro perpendicular ao diâmetro AB já traçado.
Utilizando a técnica aprendida no artigo “Retas perpendiculares que se cruzam num ponto dado” tracemos a perpendicular à reta AB que passe pelo ponto C.
Utilizando a técnica aprendida no artigo “Retas perpendiculares que se cruzam num ponto dado” tracemos a perpendicular à reta AB que passe pelo ponto C.
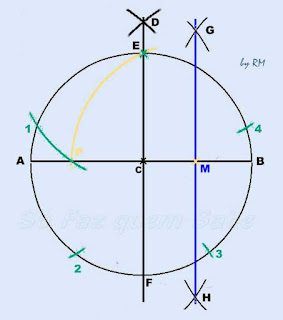
Pegamos o compasso e, com um raio maior que BC, com centro em A e B, fazemos dois arcos acima da circunferência, que ao se interceptarem definirão o ponto D.
Em seguida, com a régua, traçamos a reta que passa pelos pontos D e C que é a perpendicular que queríamos.
Com isto, estão definidos os pontos E e F (intersecção da reta DC com a circunferência).
Com isto, estão definidos os pontos E e F (intersecção da reta DC com a circunferência).
Passo 4
Agora, utilizando o que aprendemos no artigo "Mediatriz e ponto médio de um segmento" vamos obter o ponto M, ponto médio do raio BC.
Pegamos o compasso, e com centro em B e C traçamos os arcos acima e abaixo do segmento BC achando os pontos G e H que determinarão a mediatriz e consequentemente o ponto médio M do raio BC.
Passo 5
Em seguida, com centro no ponto M e com uma abertura do compasso até o ponto E, descreve-se um arco até o diâmetro horizontal AB determinando o ponto P.
Passo 6
A distância do ponto E ao ponto P é a medida da corda correspondente ao arco que é a quinta parte da circunferência.
Fazendo-se centro em E, transporta-se a distância EP para a circunferência e obtém-se o ponto 1. O arco 1E é a quinta parte da circunferência.
Fazendo-se centro em E, transporta-se a distância EP para a circunferência e obtém-se o ponto 1. O arco 1E é a quinta parte da circunferência.
Passo 7
A partir do ponto 1, marca-se mais três vezes este comprimento (1E) e determina-se os pontos 2, 3 e 4.
Passo 8
Os pontos 1, 2, 3, 4 e E são os vértices do pentágono regular inscrito nessa circunferência.







Ótima explicação!!
ResponderExcluiraprendi isso na decada de 60, mas havia esquecido, ótima explicação as figura s ja foram suficientes para recordar, precisava desenhar uma estrela de 5 pontas, ótima explicação de geometria básica. obrigado
ResponderExcluirFoi bom recordar... vou ensinar aos meus netos.
ResponderExcluirObrigada.
Grata! Relembrar é bom.Precisava de um pentágono para fazer lanternas prá turma de meu neto.
ResponderExcluirLegal, agradeço ajudou a relembrar, precisava desenhar uma estrela de 5 pontas. Muito boa a explicação. Valeu👍
ResponderExcluirObrigado. Precisava dividir um queijo em 5 pedaços. Deu muito certo!
ResponderExcluirMuito obrigado
ResponderExcluirmuito bem explicado, não lembrava mais mas agora mãos a obra vou fazer um calendoscopio para as crianças de 5 lados sendo que ja fiz um de tres lados ficou otiomo! Vovozada vamos alegrar os netos kkkkk
ResponderExcluirmuito bom, parabéns pelo recordar....
ResponderExcluirAmei muito
ResponderExcluirfoi muito bom gostaria de fazer isso outras e outras vezes . amei
ResponderExcluirFoi muito prático, e compreensivo
ResponderExcluirMuito obrigado pela disponibilidade ao conteúdo.Aprendi muito