Côncavo e convexo na geometria. Curvas, superfícies, ângulos e polígonos.

by Roberto M.

O que é curva côncava? E curva convexa? Como descobrir se uma superfície é côncava ou convexa? Qual é o conceito de ângulo côncavo e ângulo convexo? Qual a diferença entre polígono côncavo e polígono convexo?

A geometria está apoiada nos conceitos elementares ou primitivos de ponto, reta e plano. A partir deles e com a ajuda de alguns postulados, axiomas definições e teoremas constrói-se todo o mundo mágico dos estudos geométricos.

Hoje vamos falar de algumas definições da geometria. Vamos definir figuras côncavas e figuras convexas.

CURVAS CÔNCAVAS

Chamamos de curva côncava, aquela na qual qualquer segmento de reta unindo dois de seus pontos está mais próximo do observador que o trecho da curva entre esses pontos, ou seja, do ponto de vista do observador, haverá uma depressão na linha.

Na figura abaixo podemos ver que os segmentos AB ou CD estão mais próximos do observador que as curvas AB ou CD respectivamente. É como se a curva tivesse uma “cava” em relação ao observador.

CURVAS CONVEXAS

Chamamos de curva convexa, aquela na qual qualquer segmento de reta unindo dois de seus pontos está mais afastado do observador que o trecho da curva entre esses pontos, ou seja, do ponto de vista do observador, haverá uma elevação na linha.

Na figura abaixo podemos ver que os segmentos AB ou CD estão mais longe do observador que as curvas AB ou CD respectivamente. É como se a curva tivesse um “calombo” em relação ao observador.

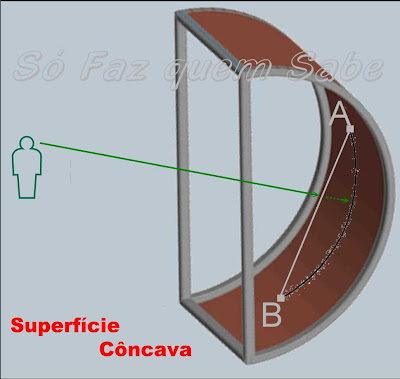
SUPERFÍCIES CÔNCAVAS

Chamamos de superfície côncava, aquela na qual qualquer segmento de reta unindo dois de seus pontos está mais próximo do observador que a curva projetada por essa reta na superfície, ou seja, do ponto de vista do observador, haverá uma depressão na superfície.

Na figura abaixo podemos ver que o segmento AB está mais próximo do observador que a sua projeção na superfície (curva AB). É como se a superfície tivesse uma “cava” em relação ao observador.

SUPERFÍCIE CONVEXA

Chamamos de superfície convexa, aquela na qual qualquer segmento de reta unindo dois de seus pontos está mais afastado do observador que a curva projetada por essa reta na superfície, ou seja, do ponto de vista do observador, haverá uma elevação na superfície.

Na figura abaixo podemos ver que o segmento AB está mais longe do observador que a sua projeção na superfície (curva AB). É como se a superfície tivesse um “calombo” em relação ao observador.

ÂNGULO CÔNCAVO OU NÃO CONVEXO

Chamamos de ângulo côncavo ou não convexo, aquele que possui mais de 180 graus, ou seja, a parte interna desse ângulo é maior do que a parte externa.

Se pudermos traçar pelo menos um segmento de reta, entre dois pontos internos desse ângulo e, esse segmento atravessar para o lado externo, dizemos que o ângulo é côncavo.

Na figura abaixo podemos ver que pelo menos o segmento AB atravessa para o lado externo do ângulo, logo ele tem mais de 180° e é côncavo.

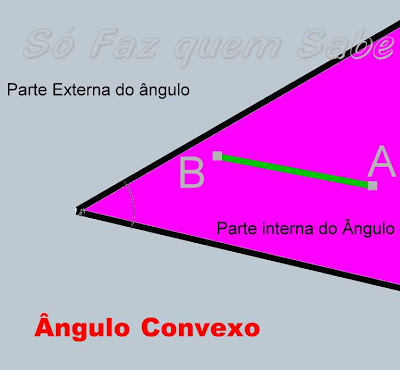
ÂNGULO CONVEXO

Chamamos de ângulo convexo, aquele que possui menos de 180°, ou seja, a parte interna desse ângulo é menor do que a parte externa.

Qualquer segmento de reta entre dois pontos internos desse ângulo estará contido na parte interna do ângulo. Não existe nenhum segmento, entre dois pontos internos, que atravessa para o lado externo.

Na figura abaixo podemos ver que qualquer que seja o segmento AB (interno ao ângulo), ele não atravessa para o lado externo, logo ele tem menos de 180° e é convexo.

POLÍGONO CÔNCAVO OU NÃO CONVEXO

Chamamos polígono côncavo ou não convexo, aquele que tem algum dos seus ângulos internos com medida maior que 180°.

Quando, num polígono, existirem pelo menos dois pontos internos a ele, que ao se unirem formam um segmento de reta que passa pelo lado de fora do polígono ele será chamado de polígono côncavo.

Um polígono diz-se côncavo quando o prolongamento de pelo menos um dos seus lados corta o polígono em duas partes.

Na figura abaixo podemos ver um polígono que tem ângulos internos maiores que 180°, onde o segmento AB passa para o lado de fora do polígono e o prolongamento do lado TU divide o polígono em duas partes. Portanto, estamos diante de um polígono côncavo.

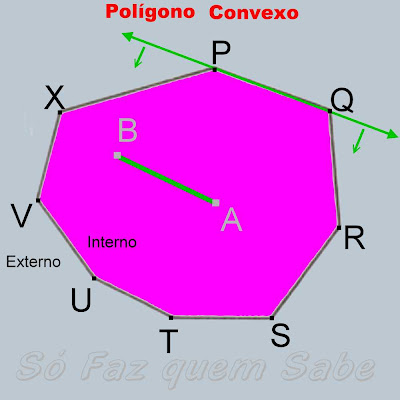
POLÍGONO CONVEXO

Chamamos polígono convexo, aquele que tem todos os ângulos internos menores que 180°.

Quando, num polígono, unirmos dois pontos quaisquer internos a ele, e o segmento de reta formado jamais passe pelo lado de fora do polígono, ou seja, fique sempre dentro da figura, ele será chamado de polígono convexo.

Um polígono diz-se convexo quando o prolongamento de qualquer dos seus lados deixa o polígono todo de um mesmo lado, ou seja, dois vértices quaisquer do polígono estarão sempre no mesmo semi-plano formado por qualquer reta que contenha um lado do polígono.

Na figura abaixo podemos ver um polígono que tem todos os ângulos internos menores que 180°, onde, qualquer que seja o segmento AB, ele ficará dentro da figura e o prolongamento do lado PQ deixa o polígono inteiro (todos os seus vértices) do mesmo lado. Portanto, estamos diante de um polígono convexo.

Observações: 1 - Uma linha reta não é côncava nem convexa.

                      2 – Uma superfície plana não é côncava nem convexa.

                      3 – Um ângulo de 180° não é côncavo nem convexo.

Artigos Recomendados:

• Diferenças entre linha, curva e poligonal. Regiões geométricas.
• Polígono. Classificação e Nomenclatura.
• Conceito de ângulo e de sua medida.
• Ângulos. Classificação e Nomenclatura. Aprenda a conhecê-los.
• Poligonal. Uma linha não linear.