Posições relativas de duas retas: concorrentes, paralelas, coplanares, reversas.

by Roberto M.

O que são retas coplanares? O que são retas concorrentes? O que são retas paralelas? O que são retas reversas?

Já vimos, anteriormente, as noções de ponto, reta e plano. Já sabemos, também, o que é um segmento de reta, ou uma semi-reta. Quem quiser relembrar, pode clicar nesses links.

Hoje vamos introduzir mais alguns conceitos e definições e falar sobre as posições relativas que duas retas podem ocupar no espaço.

Sabemos que um plano é formado por infinitos pontos e que uma reta também é um conjunto de infinitos pontos. Por isso, é fácil perceber que um plano também é formado por infinitas retas.

Para começarmos a entender as posições relativas de duas retas quaisquer, vamos, primeiramente, fazer o desenho esquemático de um plano a :

Agora vamos esquematizar algumas retas contidas nesse plano e outras que não estão contidas nesse plano.

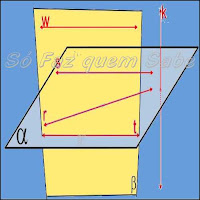
Como podemos perceber, as retas r, s e t estão contidas num mesmo plano a e as retas w e k não estão contidas num mesmo plano a.

RETAS COPLANARES

Como as retas r, s e t estão contidas num mesmo plano a  dizemos que elas são coplanares e definimos:

“Duas ou mais retas de um mesmo plano são retas coplanares”

RETAS CONCORRENTES

Se observarmos, agora, as retas coplanares r, s e t verificaremos que as retas r e s e as retas t e s se cruzam em um único ponto. Dizemos que r e s ou t e s são retas concorrentes e definimos:

“Duas retas que possuem um único ponto comum são retas concorrentes.”

RETAS PARALELAS DISTINTAS

Observemos, agora, as retas coplanares r e t. Verificamos que elas não têm, e nunca terão, nenhum ponto em comum, ou seja, elas não se cruzam. Dizemos que elas são paralelas distintas e definimos:

“Duas retas de um mesmo plano que não têm nenhum ponto em comum são retas paralelas distintas”.

RETAS PARALELAS COINCIDENTES

Pode acontecer que duas retas coplanares fiquem uma em cima da outra com todos os pontos em comum, como no caso das retas r e z da figura abaixo. Dizemos que elas são paralelas coincidentes e definimos:

“Duas retas de um mesmo plano que têm todos os seus pontos em comum são retas paralelas coincidentes”.

RETAS REVERSAS

Vamos analisar, agora, as retas k e r da figura abaixo. Verificamos que elas não estão no mesmo plano e, se observarmos bem, veremos que nunca serão coplanares, pois não há jeito de elas pertencerem a um único plano. Dizemos que essas retas são reversas e definimos:

“Duas retas serão reversas sempre que não forem coplanares, ou seja, não existirem planos que as contenham simultaneamente”.

OBSERVAÇÕES

Podemos observar, na figura abaixo, que as retas w e r não são coplanares em relação ao plano a, mas, são coplanares em relação ao plano b , portanto, w e r são retas coplanares, pois existe um plano que as contém simultaneamente.

Já as retas k e w, não pertencem, simultaneamente, nem ao plano a nem ao plano b  e, também, não há nenhum plano que consiga conter as duas retas ao mesmo tempo, portanto, elas são reversas.

Artigos Recomendados:

• Poligonal. Uma linha não linear.
• Conceito de ângulo e de sua medida.
• Ângulos. Classificação e Nomenclatura. Aprenda a conhecê-los.
• Os elementos de um triângulo. Vértices, lados e ângulos.
• Construção de um triângulo qualquer. Condição de existência de um triângulo.