by Roberto M.
Como fazemos para saber qual é o número binário que um determinado número decimal representa? Como fazer para converter um número decimal em número binário? Como fazer conversões do sistema de numeração decimal para o sistema de numeração binário?
Como vimos no artigo Sistemas Numéricos Posicionais, e no artigo Sistema de Numeração Binário, neste sistema de numeração os dígitos binários representam os coeficientes das potências de base 2.
Por exemplo, o número 23(10) é representado pela sequência de dígitos binários 10111(2)
23(10) = 16 + 0 + 4 + 2 + 1 = 1x24 + 0x23 + 1x22 + 1x21 + 1x20 = 10111(2)
10111(2) = 1x24 + 0x23 + 1x22 + 1x21 + 1x20 = 16 + 0 + 4 + 2 +1 = 23(10)
Os números com parte fracionária, da mesma forma, podem ser representados, usando-se potências negativas de dois. Assim, o número binário 101, 101(2) significa:
1x22 + 0x21 + 1x20 + 1x2-1 +0x2-2 + 1x2-3 = 5, 625
Sabe-se que, no sistema decimal (base dez), para se multiplicar um número por dez, ou seja, pela base, basta deslocar a vírgula uma casa para a direita. Se for dividir por dez, desloca-se a vírgula uma casa para a esquerda.
O mesmo ocorre com qualquer base, inclusive com a base dois.
Portanto, para se multiplicar um número por dois no sistema binário (base 2), basta deslocar a vírgula uma casa para a direita (ou para a esquerda se for divisão por dois).
Exemplos:
5 = 101
10 = 1010
20 = 10100
2,5 = 10,1
Dito isto, vamos à conversão de um número decimal para um número binário.
Dividiremos essa conversão em duas partes, primeiramente a parte inteira e depois a parte fracionária. Se o número tiver parte inteira e fracionária, calculamos cada uma separadamente.
Parte Inteira do Número
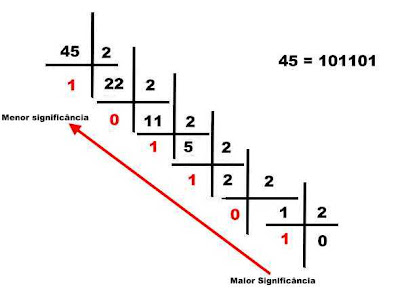
Essa conversão será feita da direita para a esquerda, isto é, determina-se primeiro o ultimo algarismo da direita (o que vai ser multiplicado por 20), em seguida o segundo algarismo (o que vai ser multiplicado por 21) e assim por diante.
No sistema de numeração binário, o número par termina em 0 e o número ímpar termina em 1. Portanto, o principal de tudo é saber se o número decimal é par ou ímpar.
Para saber se um número decimal qualquer é par ou ímpar, basta dividi-lo por dois. Se o resto for 0 o número será par. Se o resto for 1 o número será ímpar.
Assim, determina-se o primeiro algarismo da direita (que vai ser multiplicado por 20) pela simples divisão do número decimal por dois; se o resto for 0 (número par) o algarismo da direita é 0; se o resto for 1 (número ímpar) o algarismo da direita é 1.
Em seguida, para se determinar o segundo algarismo do número binário, basta lembrar que ele é a parte inteira do número original dividido por dois, abandonado o resto, pois na base dois, ao se dividir um número por dois, basta levar a vírgula para a esquerda.
Assim, pegando-se o resultado da divisão do número original por dois, abandonando o resto (que já foi utilizado para determinar o primeiro algarismo em binário), vamos verificar se ele é par ou ímpar, ou seja, dividi-lo por dois. Se for par (resto 0) o segundo algarismo será 0. Se for ímpar (resto 1), o segundo algarismo será 1.
Fazemos o mesmo processo sucessivamente, até não conseguirmos mais dividir o número por dois, determinando assim, todos os algarismos do número binário.
Para ficar mais claro, vamos a um exemplo prático:
Vamos converter o número 45 de decimal para binário.
Parte Fracionária do Número
Como vimos acima, na conversão da parte inteira do número decimal para binário, obtivemos os algarismos binários da direita para esquerda dividindo consecutivamente o número decimal por dois e utilizando-nos dos restos.
Na conversão da parte fracionária será um pouco diferente.
Agora vamos obter os algarismos binários, da esquerda para a direita e ao invés de dividir, iremos multiplicar a parte fracionária por 2.
Se o resultado dessa multiplicação for maior ou igual a 1, o primeiro algarismo será 1. Se o resultado da multiplicação for menor que 1, o primeiro algarismo será 0.
Para obtermos o segundo algarismo, pegamos a parte fracionária do resultado da primeira multiplicação (se deu maior que 1, retiramos o 1 e usamos a parte fracionária; se deu menor que 1 usamos esse resultado) e multiplicamos por 2. Se o resultado dessa multiplicação for maior ou igual a 1, o segundo algarismo será 1. Se o resultado da multiplicação for menor que 1, o segundo algarismo será 0.
Repetimos esse processo até que não exista parte fracionária após a multiplicação por 2 (ou seja, o resultado da multiplicação dá exatamente 1).
Para ficar mais claro, vamos a um exemplo prático:
Vamos converter o número 0, 625 de decimal para binário.
Se as multiplicações consecutivas da parte fracionária nunca derem como resultado exatamente 1, verificamos que essa parte fracionária é uma dízima no sistema binário.
Exemplo:
Se convertermos o número 0,8(10) para o sistema binário, obteremos como resultado o número 0,110011001100...(2).


Muito boa a explicação! Obrigada!
ResponderExcluirÓtima sua explicação
ResponderExcluirA melhor explicação! Me ajudou bastante, muito bom mesmo.
ResponderExcluirótima explicação
ResponderExcluirmassa .. muito bom
ResponderExcluirmuito boa a explicação.
ResponderExcluirA mais simples e melhor explicação de todas!
ResponderExcluirGostei da explicação mas a minha dúvida é:e quando estivermos a converter um número decimal com vírgula para binário e der uma dízima infinita. O que farei!??
ResponderExcluirApenas deu uma dízima periódica no sistema binário.
ExcluirVocê procede da mesma maneira como procederia com uma dízima periódica no sistema decimal.
olá, pode me tirar uma dúvida? Preciso converter o número 4004163 em número binário por meio da conversão direta, mas não estou conseguindo de jeito algum ;-; Se conseguir me ajudar, te agradeço muito :)
ResponderExcluirSeguindo-se o método descrito acima na "Parte inteira de um número", calcula-se que:
Excluir4004163(base 10) = 1111010001100101000011(base 2)